Modelling the stochastic behaviour of primary nucleation

Crystallization is an important separation technique, widely used, among others, in the pharmaceutical, food and fine chemistry industry, where high purity products are generally required. A vital step during the crystallization process is the formation of new particles from the parent fluid phase independent of the presence of other particles, i.e. primary nucleation. Its characteristics have relevant consequences in determining, e.g. the average size of crystal populations, the polymorph selection, the presence of fine and process yield, etc.
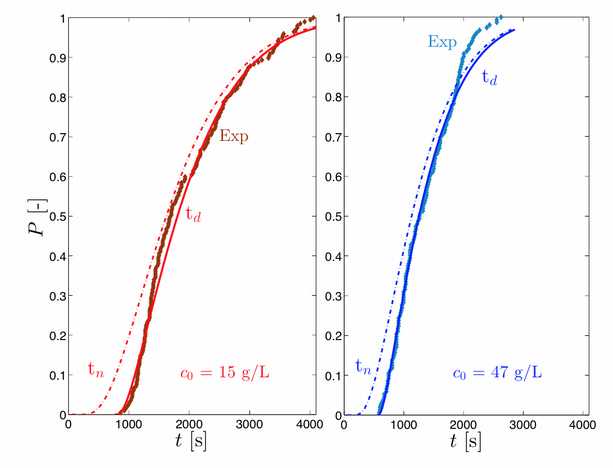
Nuclei, at the moment of their formation, are generally too small (few nm) to be directly observed by most of our current detection techniques and, hence, nucleation can only be measured indirectly through some observable quantity (e.g. the number of particles, an average length, a crystal volume fraction), which in turn defines a detection time [1, Fig.1].
Theories describing primary nucleation have been developed over more than 100 years, to provide an adequate physical and mathematical understanding for process design and development. In recent years, an increasing number of experiments revealed nucleation possesses to have an inherent stochastic nature [1,2]: this not only radically changes the previous understanding of nucleation, but also it poses a further challenge in providing a correct and useful a mathematical description of the phenomenon. Moreover, a key role in determining the stochastic behaviour of the system is played by its overall volume, which is most important for engineers during process scale-up and scale-down [2].
Our research focuses on correlating the measurable detection times with the un-measurable nucleation time and, ultimately, with the nucleation rate of engineering interest.
To pursue this goal, based on experimental data, we are developing mathematical models [1], which, on the one hand, help clarifying the physical origin of stochasticity, and, on the other hand, properly correlate the stochastic formation of primary nuclei with detection times, allowing to measure average properties and correctly design crystallization processes.
Numerical investigations have been used to study crystal nucleation at molecular level [3], while both numerical and experimental tests have been performed to assess the role of intrinsic stochasticity in systems of increasing size, and the influence of initial and boundary conditions on the outcome of nucleation (initial concentration and temperature, system volume, cooling profile, mixing…).